3.1.4 Linear Algebra and Vectors

Linear algebra is the branch of mathematics dealing with vectors, matrices, and linear transformations – essentially the "language" for expressing multidimensional data relationships. It forms the backbone of many modern AI techniques, enabling efficient representation and manipulation of high-dimensional data. From representing images and text as numerical vectors to optimizing complex deep learning models, linear algebra provides a foundation that is indispensable in artificial intelligence. In this post, we will build an intuition for key linear algebra concepts (like vectors, vector spaces, matrices, bases, and eigenvalues), visualize their geometric meanings, and see how they apply to AI – including examples in neural networks (forward/backpropagation), principal component analysis, and natural language word embeddings.

Vectors and Vector Spaces

A vector is a mathematical object with both magnitude and direction. Geometrically, we can picture a vector as an arrow pointing from one point to another in space. For example, a 2-dimensional vector v can be written as v = [x, y], indicating a displacement x in the horizontal direction and y in the vertical direction. Algebraically, a vector can be thought of as an ordered list of numbers (its components). Vectors exist in various dimensions: the 2D plane, 3D space, or higher-dimensional spaces used in machine learning to represent data (e.g. a 100-dimensional word embedding vector). Crucially, vectors can represent many things – positions, velocities, word meanings, pixel intensities – as long as we can assign numerical components.

A collection of vectors can form a vector space, which intuitively is a set of vectors closed under addition and scalar multiplication. In any vector space, a subset of basis vectors can be identified such that they are linearly independent and span the entire space. For instance, in 3D space, the standard basis is typically {(1,0,0), (0,1,0), (0,0,1)} – any 3D vector can be expressed as a linear combination of these basis vectors. The number of basis vectors is the dimension of the space. This concept of basis is powerful: it means we can describe vectors in terms of coordinates relative to a basis. In applied AI, features of data can be thought of as components of a data vector in a high-dimensional feature space, and choosing a good basis (or transforming to one, as in PCA) can simplify problems.

Operations on Vectors

Vectors can be added and scaled, operations that correspond to intuitive geometric manipulations:

• Vector Addition: To add two vectors, we add their components element-wise. Geometrically, place the tail of vector b at the head of vector a, then a + b is the arrow from the tail of a to the head of b. This is often visualized by the parallelogram law – a + b forms the diagonal of a parallelogram with sides a and b. Figure 1 illustrates this: two vectors P (purple) and Q (black) are represented as adjacent sides of a parallelogram, and their sum R (pink) is the diagonal originating from the same point. In this example, the resultant vector R combines the effects (direction and magnitude) of P and Q, and we can see that P + Q = Q + P (vector addition is commutative, as the parallelogram’s diagonal is independent of order).

Figure 1

• Scalar Multiplication: Multiplying a vector by a scalar (a single number) stretches or compresses the vector’s magnitude and/or reverses its direction if the scalar is negative. For example, multiplying v = [x, y] by 2 yields 2v = [2x, 2y], a vector in the same direction as v but twice as long. A scalar of -1 gives the opposite vector (same magnitude, opposite direction). In AI, scaling vectors is often used for normalization, such as scaling a weight update by a learning rate.

• Dot Product (Inner Product): The dot product of two vectors produces a scalar and reflects how “aligned” two vectors are. Algebraically, for two vectors a = [a1, a2, ..., an] and b = [b1, b2, ..., bn], the dot product is calculated as:

  a · b = a1×b1 + a2×b2 + ... + an×bn

  Geometrically, the dot product is also given by:

  a · b = |a| × |b| × cos(θ)

  where |a| and |b| are the magnitudes (lengths) of the vectors and θ is the angle between them. The dot product is at its maximum when the two vectors point in the same direction (θ = 0°, cos(θ) = 1) and is zero when the vectors are orthogonal (θ = 90°, cos(θ) = 0).

  In machine learning, the dot product is a fundamental operation: it is used in computing projections, similarities (cosine similarity is essentially a normalized dot product), and in the neurons of neural networks (where a neuron computes a weighted sum — a dot product — of inputs and weights). If the dot product of two non-zero vectors is zero, the vectors are said to be orthogonal, meaning they are at 90° to each other and share no directional similarity.

• Norm (Magnitude): The length of a vector v, also called its norm and often denoted as |v|, is calculated as the square root of the dot product of v with itself. For example, for a 2D vector v = [x, y], the norm is:

  |v| = sqrt(x² + y²)

  To isolate direction from magnitude, we can normalize a vector by dividing it by its norm. This results in a unit vector (a vector with length 1) pointing in the same direction as the original vector.

Linear combinations of vectors are also crucial: a vector space allows forming new vectors as a·v + b·w (adding multiples of vectors). Any vector in the space can be described as a linear combination of basis vectors. Concepts like linear independence (no vector in a set is a linear combination of others) and span (all vectors you can reach by linear combination of a set) are the algebraic underpinning of how we represent information. In machine learning, if feature vectors are linearly independent, they convey distinct information; if not, redundancy exists. For example, one hot-encoded vectors for categories are independent, whereas one feature being the sum of two others would be a linear dependency.

Matrices and Linear Transformations

A matrix is a rectangular array of numbers (with rows and columns) that can act on vectors to produce new vectors. If a vector is an “object” in our space, a matrix is an “operator” or transformation. We often denote a matrix by a capital letter (e.g. A) and its action on a vector x by A · x.

Multiplying a matrix A that has m rows and n columns (an m-by-n matrix) with a vector x that has n entries (an n-by-1 column vector) results in a new vector y that has m entries (an m-by-1 column vector). Each value in the resulting vector y is a linear combination of the components of x. In other words, each value in y is calculated by taking one row of the matrix A, multiplying each of its values with the corresponding value in the vector x, and summing those products. This operation defines a linear transformation from an n-dimensional space (the space of vector x) to an m-dimensional space (the space of vector y).

Geometrically, matrices can rotate, reflect, shear, stretch or compress space – sometimes all at once. For example, a 2×2 matrix can rotate vectors in the plane or scale the x- and y-axes differently. We can think of a matrix as a function that takes an input vector and outputs a transformed vector. An identity matrix (1’s on diagonal, 0’s elsewhere) leaves vectors unchanged, acting as the neutral transformation. Some simple transformations include: rotation matrices (which rotate vectors by a fixed angle around the origin), scaling matrices (which stretch/compress axes), and reflection matrices (which flip orientations). Every linear transformation has an associated matrix under a given basis; conversely, every matrix represents a linear transformation.

Matrix-Vector Multiplication: The rule for multiplying a matrix by a vector corresponds to taking dot products of the matrix’s rows (or columns) with the vector. For a 2×2 matrix acting on a 2D vector:

$$\begin{pmatrix}a & b\\ c & d\end{pmatrix} \begin{pmatrix}x \\ y\end{pmatrix} = \begin{pmatrix}ax + by \\ cx + dy\end{pmatrix},$$

which gives a new 2D vector. 

Each value in the resulting vector is a linear combination of the components of the input vector. This means that to compute each output value, we multiply each element in a row of the matrix with the corresponding element in the input vector and then sum the products.

Alternatively, if we think of the matrix as a set of column vectors, then multiplying the matrix by the input vector is equivalent to forming a new vector by summing the columns of the matrix, each scaled by the corresponding value in the input vector. For instance, if the input vector has components a, b, and c, and the matrix has three columns, the resulting vector is:

(a × first column of the matrix) + (b × second column of the matrix) + (c × third column of the matrix).

This column-based view helps interpret how the input vector determines how much of each column vector (feature or basis pattern) contributes to the output. In neural networks, for example, the weight matrix columns might represent learned features, and the input vector determines how strongly each feature contributes to the neuron’s output.

Matrix-Matrix Multiplication and Composition: Matrices can also multiply with other matrices. If we have a matrix A (m×n) and B (n×p), the product C = A·B is an m×p matrix representing performing B then A on a vector. Matrix multiplication corresponds to function composition: applying transformation B and then A is equivalent to a single transformation C. It’s important to note that matrix multiplication is not commutative in general (A·B ≠ B·A), because performing transformations in different orders can yield different results. However, matrix multiplication is associative (A·(B·C) = (A·B)·C) and distributive over addition. The condition for multiplication is that the number of columns of the left matrix equals the number of rows of the right matrix; otherwise, the composition is not defined.

Some special matrices and properties are worth noting:

• Square Matrix: same number of rows and columns (n×n). Square matrices often represent transformations from a space to itself (e.g. 3D rotation in $\mathbb{R}^3$).

• Diagonal Matrix: only nonzero entries on the diagonal. It stretches/compresses each coordinate axis independently.

• Identity Matrix (I): a diagonal matrix of all 1’s on the diagonal. I·v = v for any vector v (the do-nothing transformation).

• Inverse Matrix: for a square matrix A, the inverse A⁻¹ (if it exists) satisfies A⁻¹·A = I. Inverse transformations “undo” the effect (e.g. rotating by +θ then by –θ).

• Transpose (Aᵀ): flips a matrix over its diagonal (rows become columns). In linear algebra for AI, transposes show up when switching between viewing something as a combination of rows vs columns, or in converting a column vector representation to a row vector. For example, in backpropagation, the transpose of a weight matrix is used to propagate gradients backward through layers.

In data science, matrices are used to represent datasets (e.g. a design matrix with samples as rows and features as columns) and linear mappings between feature spaces. Solving a system of linear equations A·x = b (common in linear regression normal equations or optimization) involves matrix techniques such as Gaussian elimination or matrix inverses. Efficient libraries (BLAS, NumPy, etc.) leverage the structure of matrices to perform massive numbers of operations quickly in machine learning algorithms.

Eigenvalues and Eigenvectors

One of the most insightful concepts in linear algebra is that of eigenvalues and eigenvectors. Given a linear transformation represented by a square matrix A, an eigenvector of A is a non-zero vector v that, when A acts on it, results in a scaled version of v—that is, the direction of v remains unchanged. The scaling factor is called the eigenvalue. In equation form:

$$A\,v = \lambda\,v,$$

This means that applying the matrix to v stretches or compresses v by the factor lambda, and possibly flips its direction if lambda is negative, without changing its direction.

Geometric Intuition: Imagine matrix A applying a transformation (such as rotation and scaling) to every vector in a space. Most vectors will change direction. However, certain special directions exist where vectors only get scaled, not rotated. Vectors along these directions are eigenvectors of A, and the amount they are scaled is their corresponding eigenvalue. These eigenvectors represent the principal axes of the transformation. For example, if matrix A stretches space by a factor of 2 in one direction and by a factor of 4 in a perpendicular direction, then a vector aligned with the first direction has eigenvalue 2, and one in the second direction has eigenvalue 4. Any vector not aligned with those directions will change direction under A.

Finding Eigenvalues and Eigenvectors: To find eigenvalues and eigenvectors of a matrix, solve the equation:

A v=λ v,

Rewriting gives:

(A - λI) × v = 0

A non-trivial solution exists only when the determinant of (A - λI) is zero. This determinant yields a polynomial in lambda, called the characteristic polynomial. The roots of this polynomial are the eigenvalues. Plugging each eigenvalue back into the equation (A - λI) × v = 0 lets us solve for the corresponding eigenvector(s).

A square matrix with size n by n has at most n eigenvalues (including multiplicities). Not every matrix has n distinct eigenvectors. If a matrix is diagonalizable, it can be written as A = P × D × P⁻¹, where D is a diagonal matrix containing the eigenvalues, and the columns of P are the eigenvectors.

Example: Consider the matrix:

A = [ [2, 0], [0, 4] ]

This matrix stretches the x-axis by a factor of 2 and the y-axis by a factor of 4.

Applying A to vector v1 = (2, 0): A × v1 = (4, 0) = 2 × (2, 0) So v1 is an eigenvector with eigenvalue 2.

Applying A to vector v2 = (2, 2): A × v2 = (4, 8) This result is a different direction than v2, so v2 is not an eigenvector.

The directions along the x-axis and y-axis are eigendirections, with corresponding eigenvalues 2 and 4, respectively. There are no other invariant directions for this matrix.

Applications: Eigenvalues and eigenvectors are widely used in AI:

• Principal Component Analysis (PCA): Used for dimensionality reduction. The eigenvectors of the data’s covariance matrix represent the directions of maximum variance, and eigenvalues quantify how much variance is captured.

• Spectral Clustering: Clustering using the eigenvectors of a similarity matrix.

• Markov Chains and PageRank: The dominant eigenvector of the transition matrix gives the stationary distribution.

• Quantum Mechanics: Eigenvectors and eigenvalues describe physical states and observables.

• Stability Analysis: The eigenvalues of the Jacobian matrix of a system indicate whether an equilibrium point is stable.

• Deep Learning: While not computed explicitly during training, the spectrum of eigenvalues of the Hessian matrix or weight matrices provides insights into training dynamics and generalization.

Understanding eigenvalues and eigenvectors equips AI practitioners to analyze and interpret complex transformations, revealing structure and patterns in high-dimensional data.

Geometric Intuition and Visualization

Algebraic definitions are powerful, but geometric intuition often cements understanding. Let’s interpret the above concepts visually:

• Visualizing Vectors: We saw that a 2D or 3D vector can be drawn as an arrow from the origin to a specific point in space. For example, in two dimensions, a vector can be represented as an arrow from the origin (0,0) to the point (x, y). In three dimensions, the vector would extend from the origin (0,0,0) to the point (x, y, z). The length of the arrow indicates the vector's magnitude (or length), while its angle(s) relative to the coordinate axes indicate its direction.

  Vector addition can be visualized using the tip-to-tail method. When adding two vectors, place the tail of the second vector at the head (tip) of the first vector. The resulting vector (sum) is then drawn from the tail of the first vector to the head of the second vector. This forms a parallelogram when both vectors are also placed tail-to-tail. The diagonal of this parallelogram represents the sum of the two vectors.

  Vector subtraction can be visualized in a similar way. The vector a - b is the vector that, when added to b, results in a. This means you draw an arrow from the head of b to the head of a. This subtraction operation shows how the two vectors differ in both direction and magnitude.

  These visual representations help clarify some important properties of vectors:

  • Commutativity: a + b = b + a — the order of addition does not affect the result.

  • Associativity: (a + b) + c = a + (b + c) — the grouping of vectors in addition does not affect the result.

  Understanding these visual and geometric interpretations of vectors supports a more intuitive grasp of how they are manipulated in various mathematical and applied contexts, including physics and artificial intelligence.

• Linear Combinations and Span: Geometrically, multiplying a vector by scalars gives all points on the line through the origin in that vector’s direction. Adding two vectors gives a parallelogram. All linear combinations of two non-collinear vectors span a plane (a 2D subspace). For three vectors in three-dimensional space, if they’re not all co-planar, their linear combinations fill three-dimensional space. If one vector lies in the span of the others, then geometrically it is coplanar or collinear with them, indicating redundancy. In two-dimensional space, a single vector spans a line; two vectors can span the whole plane if they’re not parallel. In higher dimensions, we can’t easily draw the relationships, but the idea generalizes: span is the space of all reachable points by scaling and adding given vectors.

• Matrices as Transformations: Picture a set of grid lines in the plane (a square grid). Applying a matrix transformation A to every point will deform this grid, possibly into a tilted, scaled grid (if A is invertible, the result is still a grid, just skewed). For example, a rotation matrix will turn the grid without changing shape, a scaling matrix will make the grid rectangles wider/narrower, and a shear matrix will slant the grid parallelograms. Figure 2 illustrates a simple linear transformation in 2D: a principal component projection. In Figure 2, the green arrow u represents a certain direction (unit vector) in the original space, and the red arrow P₁ is an example data vector. The blue line dropping from P₁ onto u is the projection of that data point onto the direction u. This blue segment represents the coordinates of P₁ in the 1-dimensional subspace spanned by u. Geometrically, projection is “shadow casting” onto a line. If we chose u to be an eigenvector of a data covariance matrix, that projection captures as much variance as possible. Indeed, principal component analysis finds an optimal axis (like u) to project high-dimensional data onto a lower dimension with minimal information loss. In the figure, u is shown as the “Principal Component” direction, and projecting points onto u (the blue line) simplifies the data while preserving key variance.

Figure 2:

Figure 2: Geometric interpretation of projection onto a principal component. In this 2D example, the green vector u is the first principal component (eigenvector of the data’s covariance matrix). A sample data point P₁ (red) is projected onto u, yielding the point on u (blue) that corresponds to P₁’s coordinate in the 1D reduced space. By choosing the direction u that maximizes variance (largest eigenvalue), PCA ensures that the projection (blue) retains as much information from P₁ as possible.

• Eigenvectors: If we visualize a linear transformation with an eigenvector, imagine a shape (like an ellipse or a line) aligned with that eigenvector. After transformation, that shape will stretch or shrink along the same line, rather than rotate. For a 2×2 matrix, one can draw an arbitrary vector and see how it moves under the transformation; by adjusting the vector to where the output is parallel to the input, you’ve found an eigenvector direction. If we had an animation, eigenvectors would appear as directions where the motion is purely in/out along the line. For instance, in a simple stretching matrix, the x and y axes (if they’re eigenvectors) would stretch in place, whereas a diagonal line would rotate toward whichever axis stretches more strongly. Although we won’t dive deeper into visuals here, tools exist (like setosa.io’s eigenvector visualizations) which show these invariant directions clearly.

• High-dimensional intuition: We can’t directly visualize vectors beyond 3D, but we often use lower-dimensional projections. For example, word embeddings in NLP might be 100-dimensional vectors – not visualizable – but we can apply PCA or t-SNE to get a 2D plot of these word vectors. Words with similar meanings cluster together in these plots, reflecting that their 100D vectors were close. One famous semantic example: king – man + woman ≈ queen. This vector arithmetic implies that the difference between king and man (which represents the concept of royalty minus male) when added to woman yields a vector near queen – suggesting these words’ embeddings encode gender and royalty linearly. Such relationships are easiest to “see” when reduced to 2D: you’d find king and queen points, and man and woman points, with the vector from man to king roughly parallel to that from woman to queen. These geometric analogies are a big reason vectors are so useful in AI: they enable reasoning in vector spaces with simple arithmetic.

Applications in AI

Linear algebra isn’t just abstract math – it’s the engine under the hood of virtually all AI algorithms. Here we connect the concepts to concrete use cases:

Neural Networks and Deep Learning (Forward Pass & Backpropagation)

At the heart of neural networks lies linear algebra. A simple feed-forward neural network layer computes y = W·x + b, where x is the input vector (activations from the previous layer), W is a weight matrix, b is a bias vector, and y is the output vector (activations for the next layer). This operation is just matrix-vector multiplication (plus vector addition for the bias). Each neuron's weighted sum is a dot product between the input and that neuron's weight vector. The entire layer can be seen as a linear transform W applied to the input vector, followed by adding b (an affine transformation). Multiple layers compose these linear operations with non-linear activation functions in between, but the linear parts are crucial: they are what the network “learns” (the weights). As one source succinctly puts it: at their core, neural networks involve multiplying input data by weight matrices, adding biases, and applying activation functions – all operations defined by linear algebra.

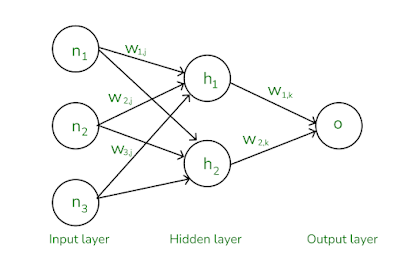Figure 3

Figure 3 shows a small neural network diagram with an input layer (neurons labeled as n1, n2, n3), one hidden layer (neurons labeled as h1 and h2), and a single output neuron labeled as o. The connections between these layers are represented by weights. The weights w1j, w2j, and w3j connect the input neurons to the hidden neurons, and the weights w1k and w2k connect the hidden neurons to the output neuron.

This neural network can also be represented using matrix notation. Suppose the input vector is written as n = [n1, n2, n3]^T (a column vector), and the hidden layer outputs are represented as h = [h1, h2]^T. Then, the activation of the hidden layer can be expressed as:

h = sigma(W1 * n) \where W1 is a 2 by 3 matrix representing the weights from the input layer to the hidden layer, and sigma denotes the activation function applied element-wise to the resulting vector.

Similarly, the output o is computed as: o = sigma(W2 * h)

Here, W2 is a 1 by 2 matrix (or a row vector) containing the weights connecting the hidden layer to the output neuron, and again sigma represents the activation function.

This formulation shows how the forward pass in a neural network is built on matrix multiplications followed by non-linear activation functions, highlighting the fundamental role of linear algebra in deep learning.

Why is this efficient? The reason is that linear algebra enables bulk operations. Instead of calculating each neuron's output in isolation, we perform matrix multiplications, which modern libraries (like BLAS) and hardware (especially GPUs) accelerate massively in parallel. For example, when training with a batch of 100 input vectors, we can stack these inputs into a single input matrix and multiply by the weight matrix at once. This approach saves time and memory and enables faster training.

During training, neural networks use the backpropagation algorithm to compute how the loss function changes with respect to each weight in the network. This gradient information tells the optimizer how to update the weights to minimize the loss. The core operations in backpropagation are composed of linear algebra and calculus (particularly the chain rule).

Here is how it works in principle:

• The output error is computed as a vector (difference between predicted and actual outputs).

• This error is then propagated backward through the layers.

• To calculate the error in a previous layer, we multiply the current error vector by the transpose of the weight matrix from that layer.

For example, if the forward operation in one layer is:

Then in the backward pass, to compute the error propagated back to n, we multiply the gradient of h by the transpose of W1:

This reversal aligns with the chain rule from calculus. It means each layer passes the gradient backward using the transposed version of the weights it used during the forward pass.

Importantly, the gradient of each weight is calculated by multiplying the input activation vector (from the forward pass) by the error vector (from the backward pass). This is equivalent to an outer product operation, and it can also be done efficiently using matrix multiplication.

In short:

• Forward pass uses matrix multiplication to compute activations.

• Backward pass also uses matrix multiplication to compute gradients.

This reliance on matrix operations is one of the key reasons why deep learning frameworks and hardware are optimized for linear algebra. Without this efficiency, training deep neural networks with millions of parameters would be computationally infeasible.

Principal Component Analysis (Dimensionality Reduction)

Principal Component Analysis (PCA) is an algorithm that heavily uses the concepts of covariance matrices and eigenvectors. When faced with high-dimensional data, PCA finds a new basis (axes) for the data space such that:

1. The axes (called principal components) are orthogonal (perpendicular) and hence uncorrelated.

2. The first few axes capture as much variance in the data as possible.

Practically, PCA computes the covariance matrix of the data, which is always symmetric and square. It then finds the eigenvectors and eigenvalues of this covariance matrix. The eigenvectors represent the principal components — directions in the feature space along which the data has the most variance. The associated eigenvalues indicate how much variance exists along each principal component. By sorting these eigenvalues from largest to smallest, we can rank the components by their importance. We can then project the original data onto the top k principal components to obtain a lower-dimensional representation that retains most of the important information from the original data.

For instance, suppose we have data points in a 2D cloud that roughly lie along a diagonal line. PCA will identify this direction as the first principal component. A perpendicular direction with very little variance might be the second component. If we keep only the first component, we have effectively reduced the dimensionality from 2D to 1D, preserving most of the variance in the data. PCA performs the same type of operation in higher dimensions.

From an algebraic point of view, performing PCA involves solving the eigenvector equation:

Here, C is the covariance matrix of the dataset, v is an eigenvector, and lambda is the associated eigenvalue. If C is an n-by-n matrix, then there are n eigenvectors, each with length n. In practice, many of these eigenvalues may be near zero, indicating that the associated dimensions do not add much new information and can be discarded.

The result of PCA is typically a projection matrix, often labeled W, whose columns are the top k eigenvectors. To project a data point x into this new lower-dimensional space, we compute:

This operation — multiplying a matrix transpose by a vector — is a linear operation and illustrates that PCA performs linear dimensionality reduction by effectively rotating and shrinking the axes of the data.

In artificial intelligence and data science, PCA is widely used for both preprocessing and visualization of data. By reducing the number of dimensions, PCA helps reduce the effect of noise and the curse of dimensionality. For example:

• In image compression, PCA can identify the main patterns in an image’s pixel values and reconstruct the image using only those main patterns.

• In natural language processing, PCA (or the closely related Singular Value Decomposition, SVD) can be applied to word co-occurrence matrices to produce word embeddings. This technique is used in Latent Semantic Analysis (LSA).

• In deep learning, PCA whitening is sometimes used to normalize input features before training a model.

The strength of PCA lies in its use of linear algebra. By computing the eigen-decomposition of the covariance matrix, PCA identifies the best directions in which to describe the data. This insight allows for more efficient computation, clearer visualization, and more accurate modeling.

Word Embeddings and NLP Vector Spaces

Natural Language Processing (NLP) has been revolutionized by the idea of word embeddings – representing words as vectors such that similar words have similar vectors. Early methods like Word2Vec and GloVe effectively factorize large matrices of word co-occurrence statistics to produce a vector (say 300-dimensional) for each word in the vocabulary. These word vectors live in a high-dimensional semantic vector space where directions and distances have meaning. Linear algebra underpins both the training and the usage of these embeddings.

To generate word embeddings, one common approach (skip-gram Word2Vec) uses a neural network to learn word vectors such that words appearing in similar contexts have vectors that are close in terms of dot product or cosine similarity. GloVe, on the other hand, explicitly builds a large matrix of co-occurrence counts (words versus context words) and then factorizes the logarithm of this matrix into the product of two smaller matrices (matrix factorization is essentially solving for matrices whose product approximates the original co-occurrence matrix). Both approaches aim to optimize the word vectors so that their dot products reflect semantic similarity or relatedness.

Once we have these vectors, we can do algebra with them. The earlier example king – man + woman = queen is a famous illustration. Here the idea is that the difference between king and man (which roughly captures the concept of “male royalty minus male”) when added to woman yields something close to queen (which is “female royalty”). This works because the embedding space has formed a subspace for the gender concept and another for the royal status concept, and these add linearly. Many such analogies hold to some extent in embedding spaces (e.g. Paris – France + Japan ≈ Tokyo for capital cities).

When we want to use or analyze word vectors, we again use linear algebra:

• Calculating word similarity: we take dot products or cosine similarity of vectors.

• To find the odd word out in a list, we might sum their vectors and see which one contributes least.

• For document or sentence embeddings, we often average or sum word vectors (a linear combination).

• Techniques like PCA can be applied on embedding sets to visualize them in 2D, as noted earlier (words cluster by semantic categories or grammatical role when plotted).

Moreover, advanced language models (like Transformer-based embeddings) also rely on linear algebra at their core. The transformer's attention mechanism is essentially using dot products between query and key vectors to determine attention weights. Matrices of parameters project words into different subspaces (queries, keys, values), and the whole training is one large dance of linear algebra (plus nonlinearities), very much like a big neural network.

In summary, word embeddings highlight how representing concepts as vectors enables us to use geometric relations to reflect semantic relations. Linear algebra provides both the methods to learn these representations (matrix factorization, singular value decomposition, neural network weight optimization) and the means to manipulate them (arithmetic and comparisons in vector space). The success of NLP techniques from the 2010s onward is a testament to the power of linear algebra combined with lots of data.

Other AI Contexts:

Nearly every subfield of AI uses linear algebra:

• Computer Vision: Images are often treated as long vectors of pixel values. Transforming images (rotations, scaling) uses matrices. Convolutional neural networks use many linear operations (convolutions that can be viewed as matrix multiplications in certain cases).

• Recommender Systems: User preferences can be represented as vectors, and matrix factorization is used to decompose a large user-item rating matrix into latent factor vectors for users and items (collaborative filtering). The resulting vectors can be used to predict ratings by computing dot products (how aligned a user and item are in latent feature space).

• Robotics and Graphics: Transformations of coordinates (rotation matrices, projection matrices) are core linear algebra. Robotic dynamics often linearize systems around operating points (using Jacobian matrices).

• Optimization: Many machine learning algorithms reduce to solving systems of linear equations or finding eigenvectors and eigenvalues. A prime example is linear regression, where the solution can be computed using the so-called "normal equation." This approach solves for the vector of coefficients that minimizes the squared error between predicted and actual values. The solution formula is:

  Inverse of (Transpose of X multiplied by X), then multiplied by (Transpose of X multiplied by y)

• Graph Analytics: Graphs can be represented via adjacency matrices, and many algorithms (like spectral clustering, or finding network centrality) involve eigenvectors of those matrices.

The ubiquity of linear algebra in AI is why tools like NumPy, MATLAB, and highly optimized GPU libraries exist – they are optimized for the dense linear algebra operations that AI workloads demand. Even when using high-level frameworks (TensorFlow, PyTorch), under the hood you are constructing computations that are eventually executed as matrix operations.

Conclusion

Linear algebra and vectors form a unifying thread across the theory and practice of artificial intelligence. We started with the basics – vectors, matrices, and their operations – building from the ground up the way these elements interact algebraically and geometrically. We saw that vectors represent data or quantities in a way that allows easy manipulation, and matrices represent transformations of that data. Concepts like vector spaces, bases, and eigenvectors/eigenvalues provide a deeper understanding of how and why these transformations can be useful (for instance, revealing important patterns via PCA or stable directions via eigenvectors). Geometrically, thinking in terms of arrows, rotations, and stretches demystifies the linear algebra: it’s a way to formally capture geometry and turn it into computations.

In applied AI, linear algebra is everywhere: it’s in the equations that define a neural network’s forward pass and the gradients of backpropagation; it’s in the decomposition of a complex dataset into principal components; it’s in the embedding of a word or an image into a vector space where machines can do math with meaning. By mastering linear algebra, one gains a language to describe and solve problems in machine learning and beyond. It opens the door to understanding advanced techniques (from the simplest regressions to the latest deep learning models) on a conceptual and computational level. As AI practitioners, having this toolkit is invaluable – it allows us to reason about our algorithms (why does this network layer have the shape it does? what does an attention matrix really do?) and to leverage powerful libraries to implement solutions efficiently.

In closing, the marriage of linear algebra and AI is a perfect illustration of theory meeting practice. The theory gives us eigenvalues; the practice gives us PCA for data compression. The theory gives us matrix multiplications; the practice gives us efficient neural network training on GPUs. By strengthening your linear algebra foundations, you empower yourself to innovate and understand AI models more deeply, bridging that gap between abstract vectors and real-world intelligence.

References

1. E. Mousavi, “Linear Algebra for AI: Part 1 — Introduction to Linear Algebra in Machine Learning,” Medium, Aug. 24, 2024.

2. E. Mousavi, “Linear Algebra for AI: Part 2 — Vectors in Linear Algebra,” Medium, Aug. 24, 2024.

3. K. Caicedo, “Linear Algebra Essentials for Machine Learning Developers,” FullStack Blog, Aug. 6, 2024.

4. Wikipedia, “Dot product – Geometric interpretation,” [Online]. Available: https://en.wikipedia.org/wiki/Dot_product:contentReference[oaicite:46]{index=46}.

5. GeeksforGeeks, “Backpropagation in Neural Network,” Apr. 5, 2025.

6. GeeksforGeeks, “Principal Component Analysis (PCA),” Feb. 3, 2025.

7. Math Insight (Duane Q. Nykamp), “The parallelogram law of vector addition,” [Online]. Available: http://mathinsight.org/image/vector_parallelogram_law:contentReference[oaicite:51]{index=51}.

8. N. Malla, “King — Man + Woman = Queen: The beauty of vectors,” Towards AI (Medium), Aug. 7, 2024.

9. J. Brownlee, “A Gentle Introduction to Vectors for Machine Learning,” Machine Learning Mastery, 2018 (accessed 2025).

10. A. Geron, Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow, 2nd ed. Sebastopol, CA: O’Reilly Media, 2019, pp. 53-70 (Chapter 2: End-to-End ML Project, section on Data Preprocessing – PCA).