7 A.I. Workers for WLB

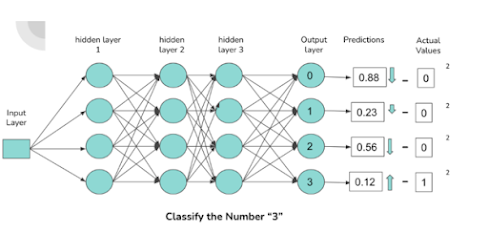
Deep learning frameworks are software libraries that provide the building blocks for creating and training neural networks. They abstract low-level details (like tensor operations and gradient computation) so developers can focus on model design and experimentation. Figure 1 illustrates a simple feedforward neural network with input, hidden, and output layers – the fundamental concept behind many deep learning models. Frameworks represent such models as computation graphs of tensor operations and automatically handle gradient backpropagation. For example, TensorFlow (pre-v2) builds a static graph at model definition time, whereas PyTorch uses a dynamic graph evaluated on the fly. This distinction – static vs. dynamic computation graphs – affects flexibility and performance of the framework. Figure 1: A simple feedforward neural network (ANN) with input, hidden, and output layers. Deep learning frameworks represent such architectures as computation graphs of tensor operations. De...

Intro Neural network training is the process of adjusting a network’s parameters (weights and biases) to minimize a loss function over training data. Conceptually, a neural network is a function  f θ ( x ) f_{\theta}(x) parameterized by θ \theta , mapping inputs x x to outputs y ^ \hat y . Training involves feeding inputs forward through the network, computing a loss (e.g., mean-squared error or cross-entropy) between y ^ \hat y and the true target y y , and then updating θ \theta to reduce this loss. The standard update rule uses Gradient Descent : θ ← θ − η   ∇ θ L ( y ^ , y ) , \theta \gets \theta - \eta \,\nabla_\theta \mathcal{L}(\hat y, y), where η \eta is the learning rate. This process repeats over many epochs , gradually improving the network’s accuracy. Training thus optimizes the cost function to find weights that best fit the data. Figure: Illustration of a feedforward neural network with 3 hidden layers classifying the digit “3.” Inputs propagate forward thr...

Neural networks come in many architectures tailored to different tasks. The simplest is the Multilayer Perceptron (MLP) , a fully connected feedforward network (no loops) that transforms inputs through layers of weighted sums and nonlinear activations. In contrast, Convolutional Neural Networks (CNNs) introduce localized weight sharing (convolutions) and pooling to process grid-like data (e.g. images). Recurrent Neural Networks (RNNs) incorporate feedback loops to handle sequences – their hidden state at time t depends on the input at t and the previous state at t–1 . Variants like LSTMs and GRUs add gating mechanisms to RNNs for better long-term memory. More recently, Transformer architectures abandon recurrence altogether in favor of self-attention, enabling highly parallel sequence modeling. Separately, Autoencoders are unsupervised nets that learn to compress and reconstruct data, while Generative Adversarial Networks (GANs) pit two networks (generator vs. discriminator) a...

3.3 Neural Networks and Deep Learning 3.3.1 What is a Neural Network? Definition & Origin: A neural network (also artificial neural network , ANN) is a computational model inspired by the brain’s neural structure. It consists of simple processing units (neurons) arranged in layers with weighted connections. Each neuron computes a weighted sum of its inputs plus a bias and applies a non‐linear activation function to produce an output. For example, a neuron’s pre-activation is  'z = ∑ w_i x_i + b' and its output is y = f(z), where f() might be a sigmoid, ReLU, or other nonlinearity. Modern neural nets can have millions of such units and hundreds of layers, and when they contain at least two hidden layers they are often called deep neural networks . Modeled loosely on the brain, a neural network is a network of interconnected “nodes” or neurons that pass signals through weighted connections. Early work on neural networks dates to McCulloch and Pitts (1943), who des...